

If we now want to assess whether a third variable (e.g., age) is a confounder, we can denote the potential confounder X 2, and then estimate a multiple linear regression equation as follows:

Where b 1 is the estimated regression coefficient that quantifies the association between the risk factor and the outcome. We can estimate a simple linear regression equation relating the risk factor (the independent variable) to the dependent variable as follows: Suppose we have a risk factor or an exposure variable, which we denote X 1 (e.g., X 1=obesity or X 1=treatment), and an outcome or dependent variable which we denote Y. Identifying & Controlling for Confounding With Multiple Linear RegressionĪs suggested on the previous page, multiple regression analysis can be used to assess whether confounding exists, and, since it allows us to estimate the association between a given independent variable and the outcome holding all other variables constant, multiple linear regression also provides a way of adjusting for (or accounting for) potentially confounding variables that have been included in the model. Again, statistical tests can be performed to assess whether each regression coefficient is significantly different from zero. In the multiple regression situation, b 1, for example, is the change in Y relative to a one unit change in X 1, holding all other independent variables constant (i.e., when the remaining independent variables are held at the same value or are fixed). Each regression coefficient represents the change in Y relative to a one unit change in the respective independent variable. Where is the predicted or expected value of the dependent variable, X 1 through X p are p distinct independent or predictor variables, b 0 is the value of Y when all of the independent variables (X 1 through X p) are equal to zero, and b 1 through b p are the estimated regression coefficients. Hypothesis testing can be done using our Hypothesis Testing Calculator.The multiple linear regression equation is as follows: The two tests for signficance, t test and F test, are examples of hypothesis tests. One of the most important parts of regression is testing for significance. This is known as multiple regression, which can be solved using our Multiple Regression Calculator. However, we may want to include more than one independent vartiable to improve the predictive power of our regression. In a simple linear regression, there is only one independent variable (x). Confidence intervals will be narrower than prediction intervals.

A prediction interval gives a range for the predicted value of y. The differennce between them is that a confidence interval gives a range for the expected value of y. In both cases, the intervals will be narrowest near the mean of x and get wider the further they move from the mean. t TestĬonfidence intervals and predictions intervals can be constructed around the estimated regression line. The only difference will be the test statistic and the probability distribution used. In simple linear regression, the F test amounts to the same hypothesis test as the t test. The test statistic is then used to conduct the hypothesis, using a t distribution with n-2 degrees of freedom. So, given the value of any two sum of squares, the third one can be easily found.
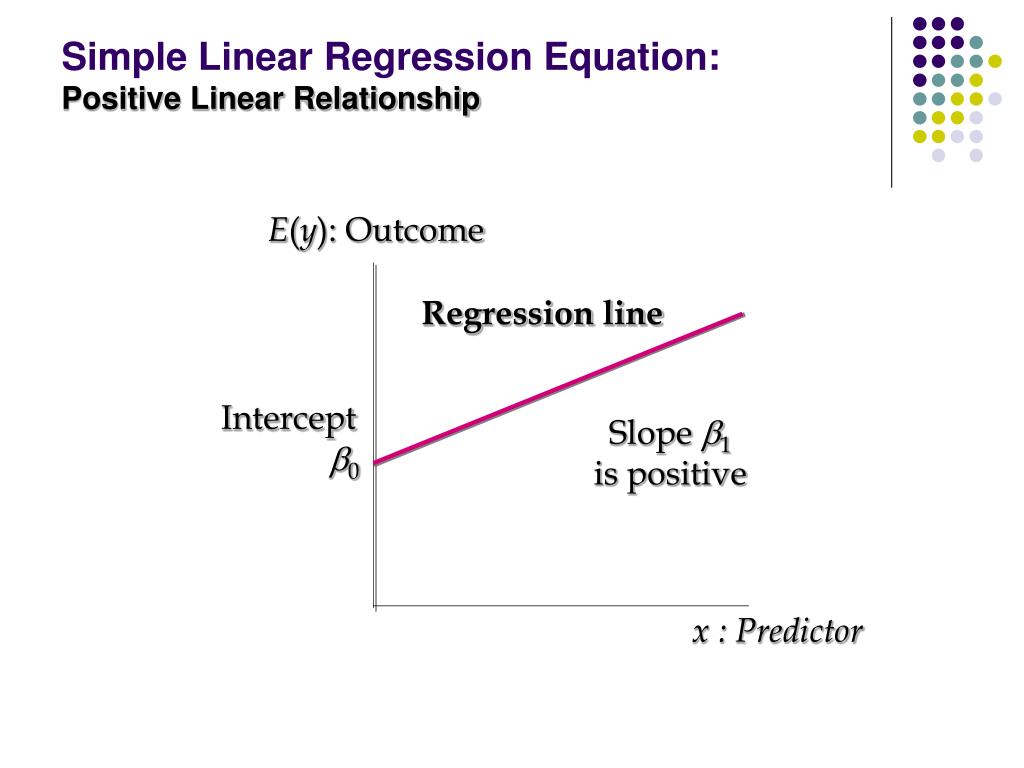
The relationship between them is given by SST = SSR + SSE. Before we can find the r 2, we must find the values of the three sum of squares: Sum of Squares Total (SST), Sum of Squares Regression (SSR) and Sum of Squares Error (SSE). The coefficient of determination, denoted r 2, provides a measure of goodness of fit for the estimated regression equation. The graph of the estimated regression equation is known as the estimated regression line.Īfter the estimated regression equation, the second most important aspect of simple linear regression is the coefficient of determination. The formulas for the slope and intercept are derived from the least squares method: min Σ(y - ŷ) 2. There are two things we need to get the estimated regression equation: the slope (b 1) and the intercept (b 0). Furthermore, it can be used to predict the value of y for a given value of x. It provides a mathematical relationship between the dependent variable (y) and the independent variable (x). In simple linear regression, the starting point is the estimated regression equation: ŷ = b 0 + b 1x.


 0 kommentar(er)
0 kommentar(er)
